由来 在初步学习了线性回归算法、逻辑回归分类算法并练习后,终于学习到了神经网络(Neural Network)。
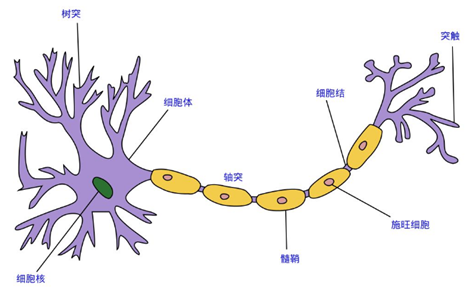
神经网络是模仿生物大脑中的神经网络设计而成,每个神经元接受外部刺激,进行一点处理,输出到下个神经元,众多神经元合作完成了对外部刺激的反应,并输出行动指令。
每个神经元都可以被认为是一个处理单元,它含有许多输入/树突 (input/Dendrite),并且有一个输出/轴突(output/Axon)。神经网络是大量神经元相互链接并通过电脉冲来交流的一个网络。
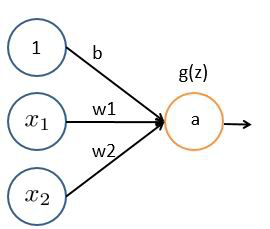
神经网络模型建立在很多神经元之上,每一个神经元又是一个个学习模型。这些神经元采纳一些特征作为输入,并且根据本身的模型提供一个输出。下图是一个以逻辑回归模型作为神经元的示例,在神经网络中,参数又可被成为权重(weight),输出节点会有一个激活函数g(z)改变其线性关系为非线性关系。
常见激活函数有:Sigmoid、ReLU、Tanh及其变种。
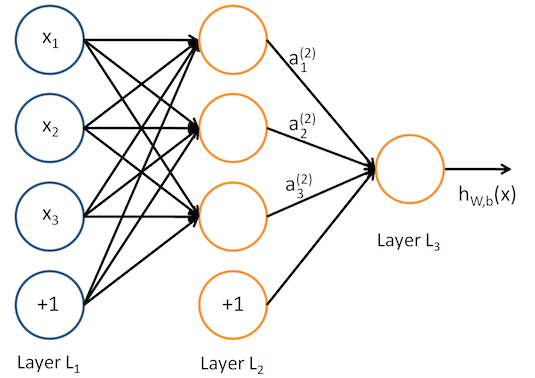
当我们增加多个神经元后,就可以形成下图的神经网络模型:
其中第一层输入层,含有x1 , x2 , x3等输入特征,我们将原始数据输入给它们。
上去就是一个简单的全连接神经网络, 下面先用神经网络模拟个逻辑与、或试试手。
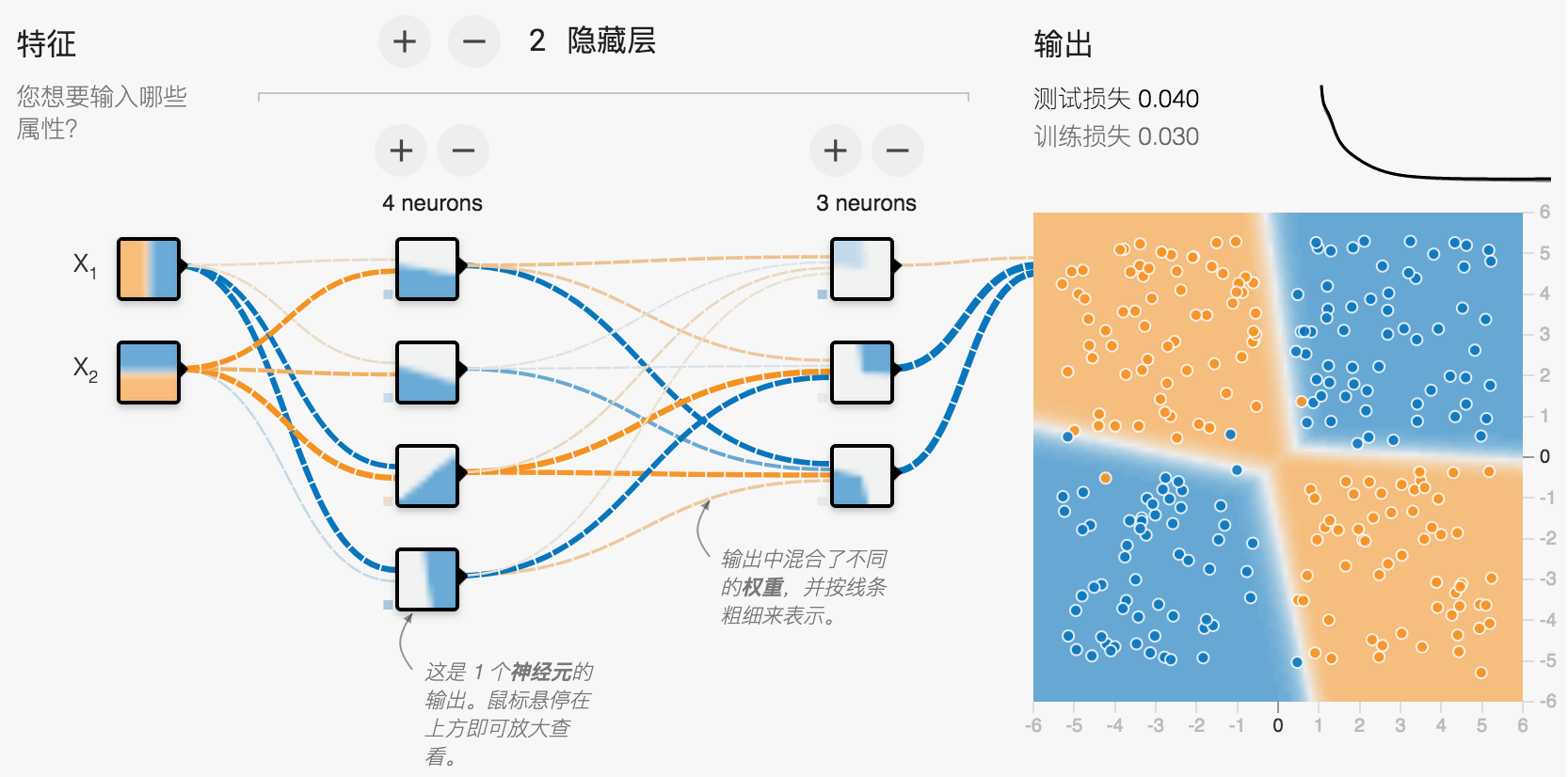
也可以先到google官方Neural Network Playground体验下,以便对nn有个直观印象。
逻辑与、或 码农对于逻辑与、或的规则很清楚,如下表:
参数1
参数2
结果:AND
结果: OR
0
0
0
0
0
1
0
1
1
0
0
1
1
1
1
1
我们需要的训练就是输入参数后能输出1或者0的结果,与逻辑二分类算法有点像,但是神经网络使用不同的损失函数来训练。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 # 首先准备样本共4个,有特征x1、x2,x0是bias,固定值1。 x0 = np.array([1, 1, 1, 1], dtype=np.float32) x1 = np.array([0, 0, 1, 1], dtype=np.float32) x2 = np.array([0, 1, 0, 1], dtype=np.float32) # 然后准备目标值target if arg_type == 'AND': target = np.array([0, 0, 0, 1], dtype=np.float32) else arg_type == 'OR': target = np.array([0, 1, 1, 1], dtype=np.float32) # 把特征和目标值转成矩证以便下面使用 m_x = np.vstack((x0, x1, x2)).T m_target = np.matrix(target).T
然后写TensorFlow计算图,定义一个输入为3个节点,输出为1个节点的单一神经元网络:
1 2 3 4 5 6 7 8 9 v_w = tf.Variable(np.zeros((3, 1)), dtype=tf.float32) h_x = tf.placeholder(shape=[None, 3], dtype=tf.float32) h_target = tf.placeholder(shape=[None, 1], dtype=tf.float32) z = tf.matmul(h_x, v_w) loss = tf.nn.sigmoid_cross_entropy_with_logits(logits=z, labels=h_target) loss = tf.reduce_mean(loss) optimizer = tf.train.GradientDescentOptimizer(200) train = optimizer.minimize(loss)
最后进行训练,一次给入全部4个样本:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 sess = tf.Session() sess.run(tf.global_variables_initializer()) loss_vec = [] for step in range(401): feed_dict = {h_x: m_x, h_target: m_target} sess.run(train, feed_dict) loss_vec.append(sess.run(loss, feed_dict=feed_dict)) if step % 100 == 0: print('step=%d W=%s loss=%s' % ( step, sess.run(v_w).ravel(), sess.run(loss, feed_dict=feed_dict))) _w = sess.run(v_w).ravel() sess.close()
如果是AND,那么最后的W=[-75. 50. 50.] loss极低,只有1.0416e-11,换句话说:y = sigmoid(-75 + 50 x1 + 50 x2 )
如果是OR,那么最后的W=[-25. 50. 50.],换句话说:y = sigmoid(-25 + 50 x1 + 50 x2 )
完整代码可见:(https://github.com/qianhk/FeiPython/blob/master/Python3Test/kaiFullNN/kai_logic_and_or.py )
Mnist手写数字数据集 我们用机器学习界的Hello Word:Mnist手写数字识别来体验下全连接神经网络。
官网(http://yann.lecun.com/exdb/mnist/ ),除了有下载地址,还有各种算法历年来拿这个数据集练手的最佳纪录。
该数据集也可以通过from tensorflow.examples.tutorials.mnist import input_data自动下载,mnist = input_data.read_data_sets(‘./cache/mnist/‘, one_hot=True),指定缓存目录即可。
1 2 3 print(f'Train data size: {mnist.train.num_examples}') print(f'Validation data size: {mnist.validation.num_examples}') print(f'Test data size: {mnist.test.num_examples}')
通过上述代码可得知,训练集样本: 55000,验证集样本:5000,测试集样本10000条。
训练时可以通过xset, yset = mnist.train.next_batch(batch_size: 8)取的一批数据,xset里是特征值,yset里是目标值,单个特征的shape是(784,),即图片长宽分别为28*28,单个独热编码形式的label.shape=(10,),形如[ 0. 0. 0. 0. 0. 0. 0. 1. 0. 0.]
实现Mnist数据集训练NN 由于图片尺寸是28*28,所以输入特征有784个,因此输入层是784个节点。
我们定义一个500个节点的隐藏层。
目标值是0到9共10个数字,所以输出层是10个节点。
首先定义计算图:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 INPUT_NODE = 28 * 28 # 输入节点数量 OUTPUT_NODE = 10 # 输出节点数量 LAYER1_NODE = 500 # 第一个隐藏层节点数量 # 定义一个获取权重的方法 def get_weight_variable(shape, regularizer): weights = tf.get_variable('weights', shape, initializer=tf.truncated_normal_initializer(stddev=0.1)) if regularizer is not None: tf.add_to_collection(tf.GraphKeys.LOSSES, regularizer(weights)) return weights # 定义计算图,输入层 矩阵乘 隐藏层权重,激活函数Relu def inference(input_tensor, regularizer): with tf.variable_scope('layer1'): weights = get_weight_variable([INPUT_NODE, LAYER1_NODE], regularizer) biases = tf.get_variable("biases", [LAYER1_NODE], initializer=tf.constant_initializer(0)) layer1 = tf.nn.relu(tf.matmul(input_tensor, weights) + biases) with tf.variable_scope('layer2'): weights = get_weight_variable([LAYER1_NODE, OUTPUT_NODE], regularizer) biases = tf.get_variable("biases", [OUTPUT_NODE], initializer=tf.constant_initializer(0)) output_layer = tf.matmul(layer1, weights) + biases return output_layer
接下来写定义训练方法,使用了L2正则化和滑动平均模型以便模型可以更好的泛化到一般情况:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 def train(mnist): x = tf.placeholder(tf.float32, [None, mnist_inference.INPUT_NODE], name='x-input') y_ = tf.placeholder(tf.float32, [None, mnist_inference.OUTPUT_NODE], name='y-input') regularizer = tf.contrib.layers.l2_regularizer(REGULARIZATION_RATE) # 使用l2正则化 y = mnist_inference.inference(x, regularizer) # 使用刚刚定义的计算图 global_step = tf.Variable(0, trainable=False, name='globalStep') variable_averages = tf.train.ExponentialMovingAverage(MOVING_AVERAGE_DECAY, global_step) variables_averages_op = variable_averages.apply(tf.trainable_variables()) average_y = y cross_entroy = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=y, labels=tf.argmax(y_, 1)) cross_entroy_mean = tf.reduce_mean(cross_entroy) loss = cross_entroy_mean + tf.add_n(tf.get_collection(tf.GraphKeys.LOSSES)) # 使用指数衰减的学习率方法,这样初期学习率可略高一点提高训练速度,后面会自动慢慢的降低学习率 learning_rate = tf.train.exponential_decay(LEARNING_RATE_BASE, global_step , mnist.train.num_examples / BATCH_SIZE, LEARNING_RATE_DECAY) train_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss, global_step=global_step) # train_op = tf.group(train_step, variables_averages_op) with tf.control_dependencies([train_step, variables_averages_op]): train_op = tf.no_op(name='train') saver = tf.train.Saver() # 每1000轮迭代保存一次模型训练结果,以便恢复训练或者使用这些模型评估训练成果 with tf.Session() as sess: sess.run(tf.global_variables_initializer()) for i in range(TRAINING_STEPS): xs, ys = mnist.train.next_batch(BATCH_SIZE) _, loss_value, step = sess.run([train_op, loss, global_step], feed_dict={x: xs, y_: ys}) if i % 1000 == 0: print(f'After {step} training step(s), loss on training is {loss_value}') saver.save(sess, os.path.join(MODEL_SAVE_PATH, MODEL_NAME), global_step=global_step) print(f'After last {step} training step(s), loss on training is {loss_value}') saver.save(sess, os.path.join(MODEL_SAVE_PATH, MODEL_NAME), global_step=global_step)
当训练11000次后,损失0.06579(After last 11000 training step(s), loss on training is 0.06579054892063141)
完整代码可见:(https://github.com/qianhk/FeiPython/tree/master/Python3Test/kaiMnist/full )
评估训练过程中的模型精度 我们再写个评估代码看看准确率怎么样,评估代码可以和训练代码开两个控制台一起运行,评估代码每隔若干秒比如5秒使用验证集预测下5000个样本的准确率,当然也可以选择测试集,此处只是初步体验下预测效果。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 x = tf.placeholder(tf.float32, [None, mnist_inference.INPUT_NODE], name='x-input') y_ = tf.placeholder(tf.float32, [None, mnist_inference.OUTPUT_NODE], name='y-input') validate_feed = {x: mnist.validation.images, y_: mnist.validation.labels} # 同样要定义计算图,直接用训练里定义好的方法 y = mnist_inference.inference(x, None) # 判断预测值与样本里目标值是否相等 correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1)) accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32)) # saver = tf.train.Saver() variable_averages = tf.train.ExponentialMovingAverage(mnist_train.MOVING_AVERAGE_DECAY) variable_to_restore = variable_averages.variables_to_restore() print(f'variable_to_restore={variable_to_restore}') saver = tf.train.Saver(variable_to_restore) while True: with tf.Session() as sess: # 从训练代码里保存的模型文件中读取参数并运行预测方法 ckpt = tf.train.get_checkpoint_state(mnist_train.MODEL_SAVE_PATH) if ckpt and ckpt.model_checkpoint_path: saver.restore(sess, ckpt.model_checkpoint_path) global_step = ckpt.model_checkpoint_path.split('/')[-1].split('-')[-1] accuracy_score = sess.run(accuracy, feed_dict=validate_feed) print(f'After {global_step} training step(s), validation accuracy = {accuracy_score}') else: print('No checkpoint file found') time.sleep(EVAL_INTERVAL_SECS)
最终,在验证集上准确率是: 98.3%,效果还是很不错的,在用上了正则化及滑动平均模型后仅仅一层隐藏层就能达到比较满意的效果。如果不是用上述优化方法,可能在训练集上得到更好的效果但由于过拟合导致泛化能力不行,从而在验证集或者测试集上准确率略微下降, 视参数不同准确率可能在94%-96%左右。
Neural Network常用损失函数 在线性回归中,我们常用平方损失(又称为 L2 损失)作为损失函数, 均方误差MSE作为每个样本的平均平方损失, RMSE作为均方根误差。
在逻辑回归二分类算法中,我们常用对数损失函数作为损失函数。
而在神经网络中,我们主要是用各种交叉熵(cross_entropy)作为损失函数, 在TensorFlow中主要是末尾是tf.nn.xxxxxx_cross_entropy_with_logits的方法。
logit函数定义为:$L(p)=ln\frac{p}{1-p}$, 是一种将取值范围在[0,1]内的概率映射到实数域[-inf,inf]的函数,如果p=0.5,函数值为0;p<0.5,函数值为负;p>0.5,函数值为正。
相对地,softmax和sigmoid则都是将[-inf,inf]映射到[0,1]的函数。
常见的有如下3种:
tf.nn.sigmoid_cross_entropy_with_logits 计算网络输出logits和标签labels的sigmoid cross entropy loss,衡量独立不互斥离散分类任务的误差。
tf.nn.softmax_cross_entropy_with_logits 计算网络输出logits和标签labels的softmax cross entropy loss,在多类别问题中,Softmax 会为每个类别分配一个用小数表示的概率。这些用小数表示的概率相加之和必须是 1.0。与其他方式相比,这种附加限制有助于让训练过程更快速地收敛。
tf.nn.sparse_softmax_cross_entropy_with_logits 这个版本是tf.nn.softmax_cross_entropy_with_logits的易用版本,每个label的取值是从[0, num_classes)的离散值。
参考: 多类别神经网络 (Multi-Class Neural Networks):Softmax
TF里几种loss和注意事项
怎样理解 Cross Entropy
本文首发于钱凯凯的博客 : http://qianhk.com/2018/10/全连接神经网络训练手写图片识别/