客户端码农学习ML —— 分类评估(准确率_精确率和召回率_ROC和曲线下面积)
判断各种机器学习方法训练而成的模型输出结果的好坏,需要一些评估方法,本文简单介绍二分类算法的几种评估方法,做个总结。
首先需要有一些基本概念:对于样本来说,通常有两种类型,一种是正类别、一种是负类别,正负类别本身没有褒义贬义的含义,纯粹为了区分二分类两种不同情况。
如“有没有狼的问题”,可以认为狼来了是正类别,没有狼是负类别;再比如“肿瘤是恶性还是良性”,恶性可以作为正类型,良性作为负类别。
对于模型的预测,可以用2x2混淆矩阵来总结,该矩阵描述了所有可能出现的结果,共4种,以肿瘤问题为例:
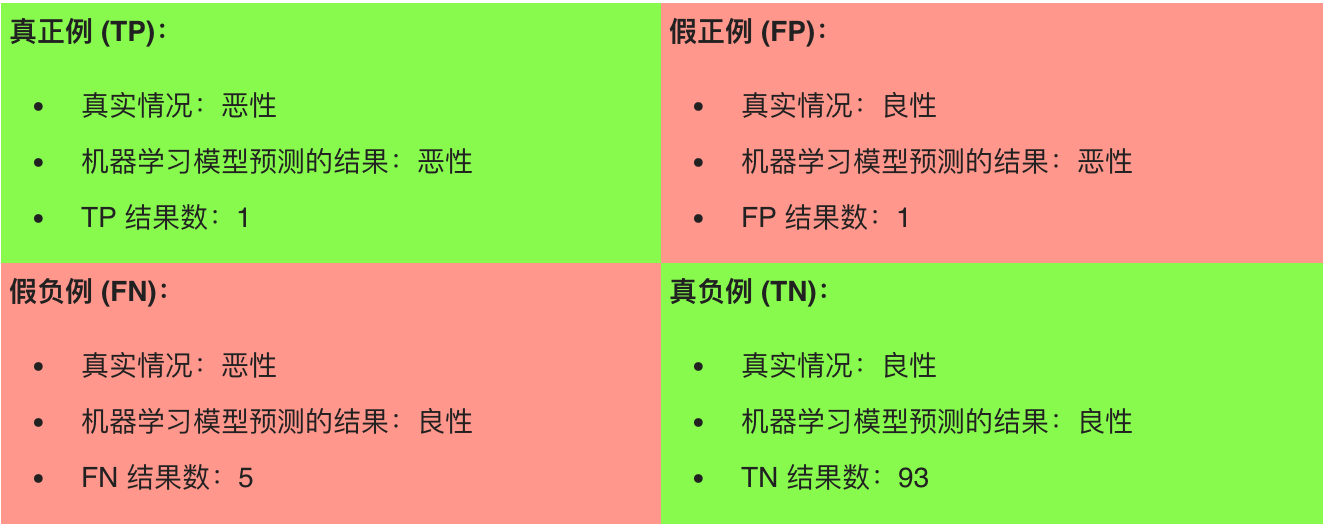
(图表来自google官方机器学习教程,简单修改了下数值)
从图表中可以看出共有100个肿瘤,其中绿色背景的预测正确,共94个(含1个恶性、93个良性),红色背景的预测错误,共6个(实际含5个恶性、1个良性)。
下面给出4个符号的定义:
真正例TP是指模型将正类别样本正确地预测为正类别。同样,真负例TN是指模型将负类别样本正确地预测为负类别。
假正例FP是指模型将负类别样本错误地预测为正类别,而假负例FN是指模型将正类别样本错误地预测为负类别。
简单的说: TP = 真正例,TN = 真负例,FP = 假正例,FN = 假负例。
准确率 Accuracy
准确率通常是我们最容易想到的一个评估分类模型的指标。通俗来说,准确率是指我们的模型预测正确的结果所占的比例。其值等于预测正确的样本数除以总样本数,取值范围[0,1]。
套用上面4个符号的定义,可以形成如下公式:
【如果看到公式是乱七八糟的字符,请刷新下网页】
$$\text{准确率} = \frac{预测准确数}{样本总数} = \frac{TP+TN}{TP+TN+FP+FN}$$
因此对于上面的图表:
$\text{Accuracy} = \frac{TP+TN}{TP+TN+FP+FN} = \frac{1+93}{1+93+1+5} = 0.94$
94%的准确性一般来说还不错,但是对于本身分类不平衡的样本来说会有很严重的问题,对于本例来说就是恶性肿瘤数本身占比肿瘤整体很少,只有6%。如果我们写个模型总是预测肿瘤为良性,那么准确率是94个良性除以样本100,结果还是94%的预测准确率,由此可以推断准确率不是个靠谱的指标。
因此科学家们定义了两个能够更好地评估分类不平衡问题的指标:精确率和召回率。
精确率 Precision 和召回率 Recall
精确率是指:在被识别为正类别的样本中,确实为正类别的比例是多少?
$$\text{Precision} = \frac{TP}{TP+FP}$$
召回率是指:在所有正类别样本中,被正确识别为正类别的比例是多少?
$$\text{Recall} = \frac{TP}{TP + FN}$$
对于上面肿瘤的例子:$\text{精确率} = \frac{TP}{TP+FP} = \frac{1}{1+1} = 0.5$,而$\text{召回率} = \frac{TP}{TP+FN} = \frac{1}{1+5} = 0.17$,可以看出精确率和召回率都很低,换句话说,识别精度不高代表识别为恶性肿瘤的可能很大几率并不是恶性肿瘤,召回率低代表很多恶性肿瘤没能识别出来。
一般来说人们希望精确率和召回率都高,最好都是100%,这样代表识别出来的样本确实都是正类别,且所有正类别都被识别出来了。但是现实中这两个指标往往是此消彼长的关系,也就是说,提高精确率通常会降低召回率值,即使不从数学上证明,从感觉上也能理解,因为这两个指标的目标刚好相反,一个要求尽可能精确,那么要抛弃掉难以决定的把握不大的样本;而另一个指标要求尽可能识别出所有的正类别,那么就可能带入把握不大的样本。可以想象下识别垃圾邮件,精确与识别全难两全。
那么如果两个模型识别样本的精确率与召回率分别是:0.6 0.6 与 0.5 0.7,那么哪个好呢?
于是数学家又定义了一个指标去计算,名叫:F score,常见的是F1 score。
F1值
F1 score 是精确值和召回率的调和均值,它的公式是:
$$ F_1 = \frac{2}{\frac{1}{recall} + \frac{1}{precision}} = 2 \cdot \frac{precision \cdot recall}{precision + recall} $$
对于极端最好的例子:精确率=1.0 召回率=1.0时, $F_1 = 2 \cdot \frac{1.0 \cdot 1.0}{1.0 + 1.0} = 1.0 $
于是对于上面的两个例子,F1 score分别是:
precision=0.6 recall=0.6时 $F_1 = 2 \cdot \frac{0.6 \cdot 0.6}{0.6 + 0.6} = 0.60 $
precision=0.5 recall=0.7时 $F_1 = 2 \cdot \frac{0.5 \cdot 0.7}{0.5 + 0.7} = 0.58 $
显然precision=0.6 recall=0.6的模型效果相对稍微好点。
ROC、曲线下面积(AUC)
除了上面的F1值外,还有方法来判断一个分类模型的好坏,且更直观,它就是ROC曲线。
ROC 曲线(接收者操作特征曲线)是一种显示分类模型在所有分类阈值下的效果的图表。该曲线绘制了真正例率、假正例率两个参数。
同样的,首先定义几个概念:
真正例率 (TPR、true positive rate) 是召回率的同义词,因此定义如下:
$$\text{TPR} = \frac{TP}{TP + FN}$$
假正例率 (FPR、false positive rate),定义如下:
$$FPR = \frac{FP}{FP+TN}$$
ROC (Receiver Operating Characteristic Curve)接收者操作特征曲线
ROC 曲线用于绘制采用不同分类阈值时的 TPR 与 FPR。降低分类阈值会导致将更多样本归为正类别,从而增加假正例和真正例的个数。
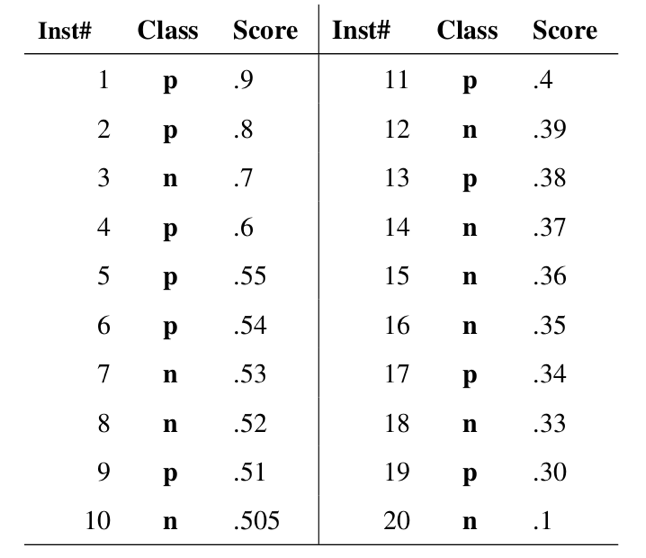
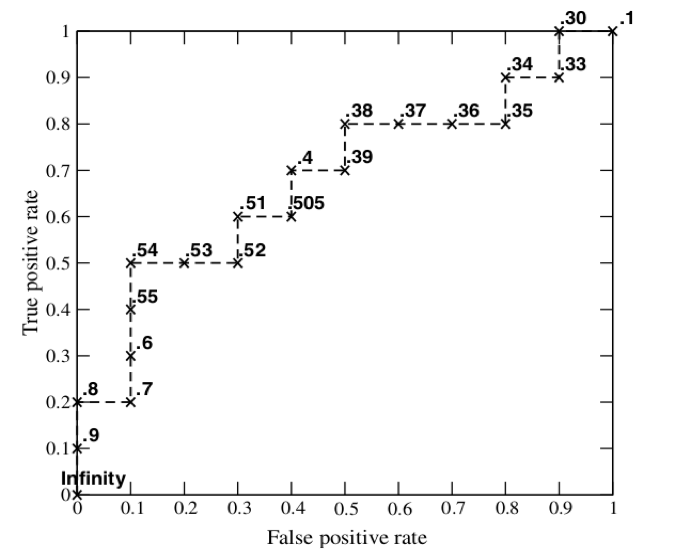
AUC (Area Under Curve) ROC曲线下面积值,也就是说,曲线下面积测量的是从 (0,0) 到 (1,1) 之间整个 ROC 曲线以下的整个二维面积。
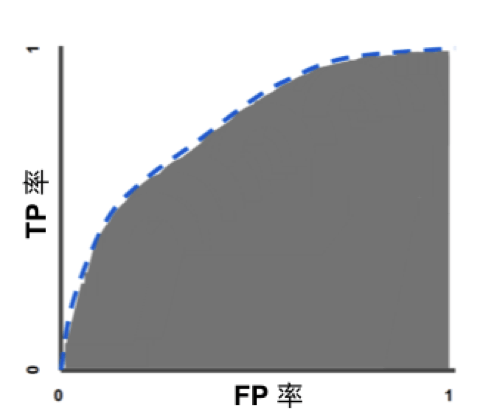
前文逻辑回归算法的一个模型可视化图:有样本及预测结果预览(左侧),还有训练时每次迭代损失值(右上角),accuracy,auc等指标(下方):
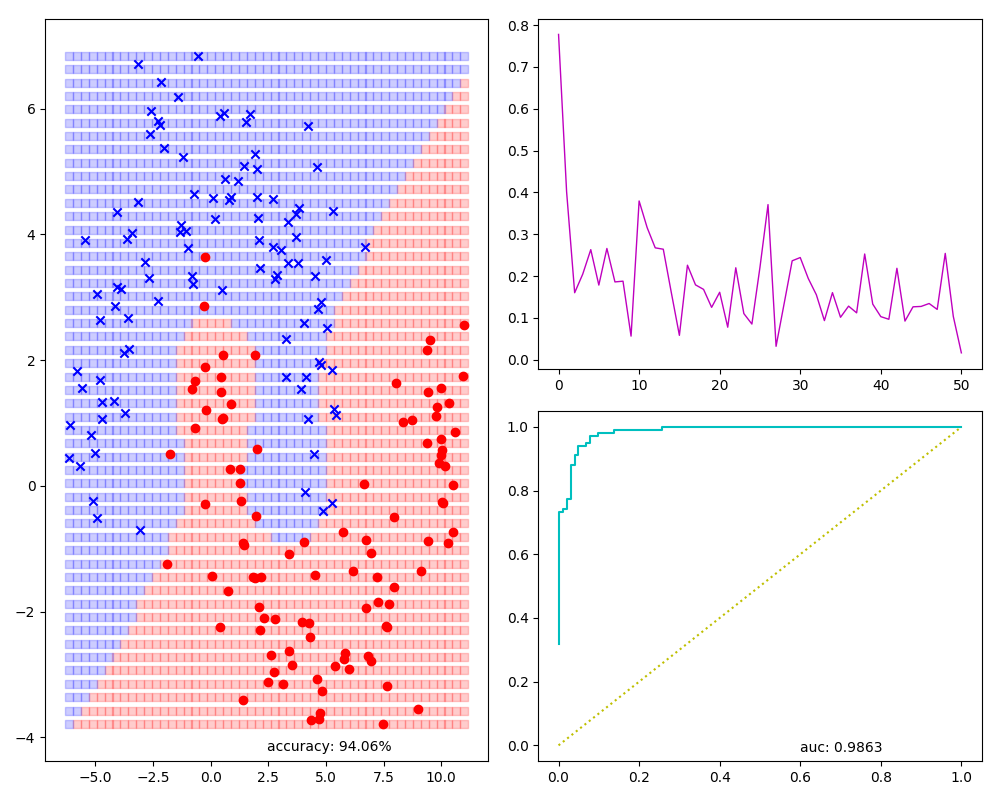
当面积是最大值1的时候,此时覆盖左上角,而左上角TPR是1.0, FPR是0.0,说明所有的正例都识别出来了,而没有一个负例被错误的识别为正例。
总结
总的来说,本文介绍的几个指标对于初学者来说还是比较绕的,先是比较直白的准确率,但是对于分类不均衡的样本来说准确率很不靠谱,于是有了精确率和召回率,但由于有两个指标,对于多个模型这两个指标差不多的情况下难以判断哪个更好于是出现了F1值,同时还有更直观的ROC曲线和曲线下面积,直接通过图形化方式直观的去看一个模型在各种分类阈值下的表现。
参考:
本文首发于钱凯凯的博客 : http://qianhk.com/2018/09/分类评估(准确率_精确率和召回率_ROC和曲线下面积)/