客户端码农学习ML —— 欠拟合_过拟合_正则化

在机器学习的训练中，欠拟合、过拟合是个绕不过去的问题，本文则试验下这两种现象，并对过拟合问题尝试使用正则化来避免，同时为了加快训练速度，对特征进行了缩放，使多个特征的值大小范围处于同一个量级，体验了一把特征缩放对训练速度的影响。

数据准备

通过numpy库创建一个数组，作为只有一个特征的样本，同时通过log函数创建目标值数组，并加点随机偏移。

1
2
3
pie_size = np.array([-2, -1, 0, 1, 2], dtype=np.float32)
pie_price = np.log((pie_size + 3) * 10)
pie_price += np.random.normal(0, 0.3, [5])

这个特征可以理解为饼的大小(1寸到5寸，为了后续计算平方、立方、高次方的数值小，防止NAN，有意减3)，价格在饼的大小基础上通过log方法得到。

后续试验假设我们并不知道这些样本的特征与标签的真正关系，而是通过增加多项式来拟合。

欠拟合

通过学习我们知道欠拟合通常是模型过于简单，不能较好的拟合训练样本，因此通过单变量来尝试拟合试试效果。

1
2
3
4
5
6
7
8
9
10
11
12
13
b = tf.Variable(0, dtype=tf.float32)
w1 = tf.Variable(0, dtype=tf.float32)

learn_rate = 0.01
target = b + w1 * pie_size
loss = tf.reduce_mean(tf.square(target - pie_price))

# 以下样本代码忽略
optimizer = tf.train.GradientDescentOptimizer(learn_rate)
train = optimizer.minimize(loss)

sess = tf.Session()
sess.run(tf.global_variables_initializer())

熟悉线性回归的可以看出这其实就是个单变量线性回归，拟合出来是一条直线，显然不能拟合出像log的图形。

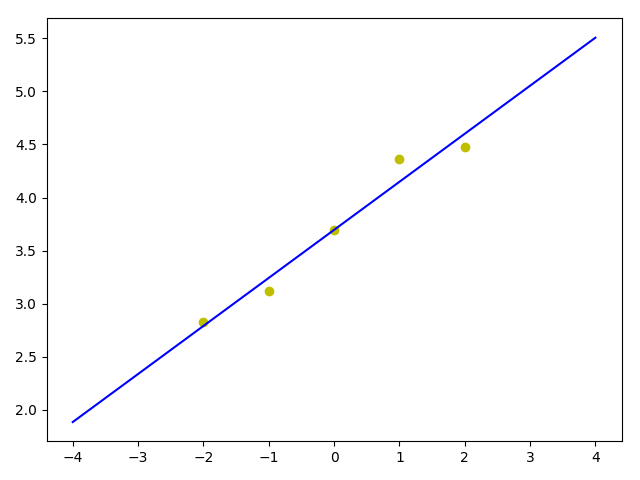
fitting_underfitting

拟合合适

相对于单变量的基础上，再增加一个变量

1
2
3
4
5
w2 = tf.Variable(0, dtype=tf.float32)

# 特征可以实现组合成平方、立方等形成新的特征，并改写成矩阵乘法更简洁
target = b + w1 * pie_size + w2 * pie_size ** 2
return tf.reduce_mean(tf.square(target - pie_price))

从下图可以看出比较接近log函数的样子了。

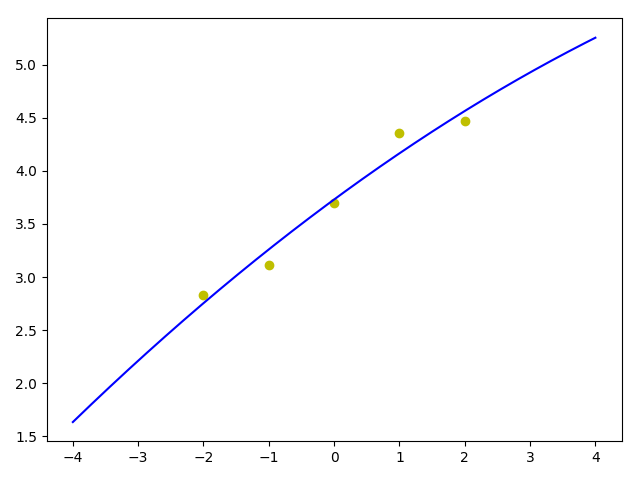
fitting_fitting_ok

过拟合

为了模拟过拟合，再增加两个变量：

1
2
w3 = tf.Variable(0, dtype=tf.float32)
w4 = tf.Variable(0, dtype=tf.float32)

无特征缩放

1
2
3
4
learn_rate = 0.0001
target = b + w1 * pie_size + w2 * pie_size ** 2
	 + w3 * pie_size ** 3 + w4 * pie_size ** 4
return tf.reduce_mean(tf.abs(target - pie_price))

有特征缩放

原始值范围是0-2， 二次方、三次方、四次方后分别最大4、8、16，所以我简单的分别除以2、4、8，将至缩放到同一量级，比较常见的算法是min-max算法，都缩放到0-1之间。

1
2
3
4
learn_rate = 0.01
# 同样，特征可以实现组合成平方、立方等多次方后再除以对应的缩放系数形成新的特征，并改写成矩阵乘法
target = b + w1 * pie_size + w2 * pie_size ** 2 / 2
	 + w3 * pie_size ** 3 / 4 + w4 * pie_size ** 4 / 8

特征缩放后，可以提高学习率，在我2014款mbp上只要2、3秒就可以完美拟合这5个样本点。

而未进行特征缩放的时候，虽然我有意选择了较小的特征数值，但由于4次方后的值较大，学习率得降低，不然训练过程中不是NAN就是损失先降低又上升，总之无法拟合。较低的学习率使得训练时长大幅增加，得到相似的结果大概需要40秒。

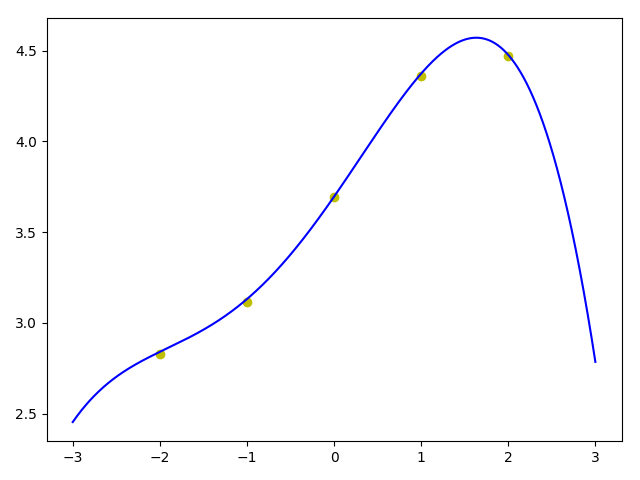
fitting_overfitting

即使不用测试集，从图中也明显看出过拟合了，虽然5个点都完美穿过，但这压根儿不像是log图形的样子，尤其是右边，本应向上却几乎直线下降了。

正则化

对于本地我们可以通过减少特征的方法避免过拟合现象，对于样本少特征多且没有明显特征可以减少的的情况我们试试正则化方法。

1
2
3
4
5
6
7
8
9
10
learn_rate = 0.001

regularization_strength = 0.2
regularization_result = regularization_strength \
                        * (tf.abs(w1) + tf.abs(w2) + tf.abs(w3) + tf.abs(w4))
target = b + w1 * pie_size + w2 * pie_size ** 2 / 2
	 + w3 * pie_size ** 3 / 4 + w4 * pie_size ** 4 / 8
loss = tf.reduce_mean(tf.abs(target - pie_price)) + regularization_result

# 最终参数值为： bias=3.6952 w1=0.4110 w2=-0.0098 w3=-0.0000 w4=-0.0099

本次通过L1正则化试验，可以看到w3几乎被降为了0，可以认为这个特征可以忽略掉了，由于增加正则化，试验下来相比单纯的仅特征缩放不用正则化，学习率要降低些，时间上有所增加。

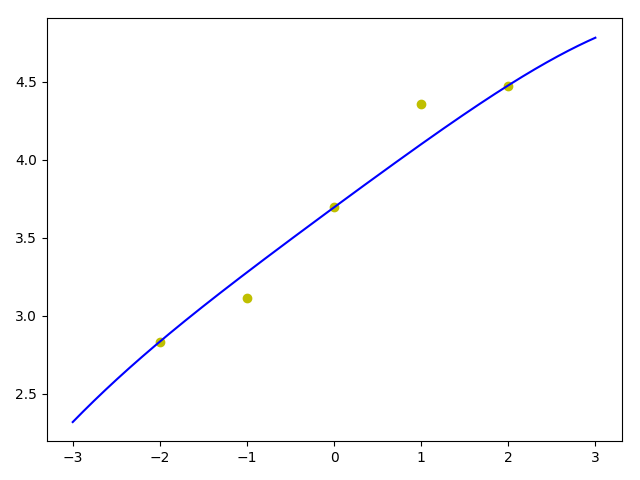
fitting_overfitting_scale_l1

可以通过调整正则化强度regularization_strength来控制拟合平滑程度。

从图形上看跟上面第二种有两个变量的情况下差不多，拟合较好，当然更严谨的需要通过测试集、验证集来验证在新数据集上的预测损失情况。

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
#!/usr/bin/env python
# coding=utf-8

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import time

np.random.seed(0)

b = tf.Variable(0, dtype=tf.float32)
w1 = tf.Variable(0, dtype=tf.float32)
w2 = tf.Variable(0, dtype=tf.float32)
w3 = tf.Variable(0, dtype=tf.float32)
w4 = tf.Variable(0, dtype=tf.float32)

pie_size = np.array([-2, -1, 0, 1, 2], dtype=np.float32)
pie_price = np.log((pie_size + 3) * 10)
pie_price += np.random.normal(0, 0.3, [5])
# print(pie_price)

regularization_strength = 0.2
regularization_result = regularization_strength \
                        * (tf.abs(w1) + tf.abs(w2) + tf.abs(w3) + tf.abs(w4))


def loss_for_underfitting():
    target = b + w1 * pie_size
    return tf.reduce_mean(tf.square(target - pie_price))


def loss_for_ok():
    target = b + w1 * pie_size + w2 * pie_size ** 2
    return tf.reduce_mean(tf.square(target - pie_price))


def loss_for_overfitting():
    target = b + w1 * pie_size + w2 * pie_size ** 2 + w3 * pie_size ** 3 + w4 * pie_size ** 4
    return tf.reduce_mean(tf.abs(target - pie_price))


def loss_for_overfitting_scale():
    # 2   4   8   16
    target = b + w1 * pie_size + w2 * pie_size ** 2 / 2 + w3 * pie_size ** 3 / 4 + w4 * pie_size ** 4 / 8
    return tf.reduce_mean(tf.abs(target - pie_price))


def loss_for_overfitting_regular():
    target = b + w1 * pie_size + w2 * pie_size ** 2 / 2 + w3 * pie_size ** 3 / 4 + w4 * pie_size ** 4 / 8
    return tf.reduce_mean(tf.abs(target - pie_price)) + regularization_result


method = 1

if method == 0:
    learn_rate = 0.01
    loss = loss_for_underfitting()
elif method == 1:
    learn_rate = 0.0001
    loss = loss_for_ok()
elif method == 2:
    learn_rate = 0.0001
    loss = loss_for_overfitting()
elif method == 10:
    learn_rate = 0.01
    loss = loss_for_overfitting_scale()
else:
    learn_rate = 0.001
    loss = loss_for_overfitting_regular()

optimizer = tf.train.GradientDescentOptimizer(learn_rate)
train = optimizer.minimize(loss)

sess = tf.Session()
sess.run(tf.global_variables_initializer())

step = 0
last_loss1 = 0
last_loss2 = 0
while True:
    step += 1
    sess.run(train)
    if step % 1_0000 == 0:
        loss_value = sess.run(loss)
        time_str = time.strftime("%H:%M:%S", time.localtime())  # %Y-%m-%d %H:%M:%S
        print(f'step={step} time={time_str} loss={loss_value:0.8f}'
              + f' bias={sess.run(b):0.4f} w1={sess.run(w1):0.4f} w2={sess.run(w2):0.4f} w3={sess.run(w3):0.4f} w4={sess.run(w4):0.4f}')
        if loss_value < 0.01:
            break
        if last_loss1 == last_loss2 and last_loss2 == loss_value:
            break
        last_loss2 = last_loss1
        last_loss1 = loss_value
    if step >= 50_0000:
        break

_b = sess.run(b)
_w1 = sess.run(w1)
_w2 = sess.run(w2)
_w3 = sess.run(w3)
_w4 = sess.run(w4)

print(f'bias={_b} w1={_w1} w2={_w2} w3={_w3} w4={_w4}')

sess.close()

best_fit = []
x_array = np.linspace(pie_size[0] - 1, pie_size[len(pie_size) - 1] + 1, 10000)
for x in x_array:
    if method < 10:
        best_fit.append(_b + _w1 * x + _w2 * x ** 2 + _w3 * x ** 3 + _w4 * x ** 4)
    else:
        best_fit.append(_b + _w1 * x + _w2 * x ** 2 / 2 + _w3 * x ** 3 / 4 + _w4 * x ** 4 / 8)

# print(f'best_fit={best_fit}')

show_plt = 1

if show_plt == 1:
    plt.figure()
plt.scatter(pie_size, pie_price, c='y', marker='o', label="pie")
plt.plot(x_array, best_fit, color='b')
plt.show()

源码地址：https://github.com/qianhk/FeiPython/blob/master/Python3Test/kaiLinear/kai_overfitting_regular3.py

参考：

吴恩达机器学习教程：
http://study.163.com/course/introduction/1004570029.htm

　

本文首发于钱凯凯的博客 : http://qianhk.com/2018/07/客户端码农学习ML-欠拟合_过拟合_正则化/

发布于 
tags:
  • { AI }
  • { 拟合 }
  • { 正则化 }