客户端码农学习ML —— 用TensorFlow实现线性回归算法

线性回归（Linear Regression）

线性回归算法是机器学习、统计分析中重要的算法之一，也是常用的相对简单的算法。

微信小游戏跳一跳某辅助程序wechat jump game，之前要事先根据屏幕尺寸填写一个按压时间与弹跳距离的比例经验值并不断人为调整，后来可通过此算法拟合按压时间与弹跳距离了, Pull Request在此。

给定由d个属性描述的点集X=(x1;x2;…;xd), 线性模型试图学得一个通过属性的线性组合来进行预测的函数，即ƒ(x)=w1x1 + w2x2 + … + wdxd + b，知道w和b后就能确定模型。

原理

我们在高中数学中已经学过只有一个属性x求待定系数的算法，即最小二乘法，一系列离散点通过最小二乘法即可确定一条回归直线ƒ(x)=kx+b，这种只有一个输入变量/特征值的问题也叫作单变量线性回归问题。

Cost Function

不同的k值，也使得预测值与实际值的建模误差不同，方差是常用的一种损失函数，也叫代价函数（Cost Function），我们的目标就是找到可以使得方差最小的模型参数。

单变量线性回归的损失函数通图形化后常类似于一个抛物线，有一个最小值。

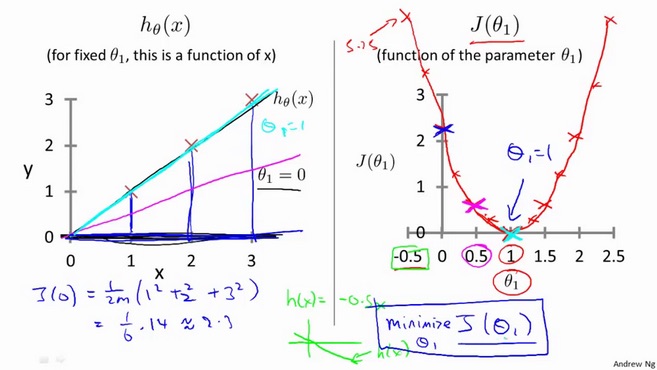
ai_cost_parabola

两个变量/特征的线性回归损失函数图形化后类似于一个碗，碗底就是最小值。

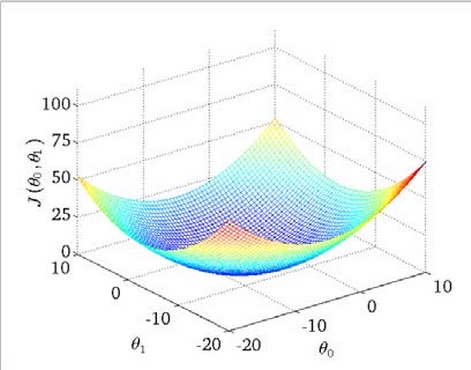
ai_cost_bowl

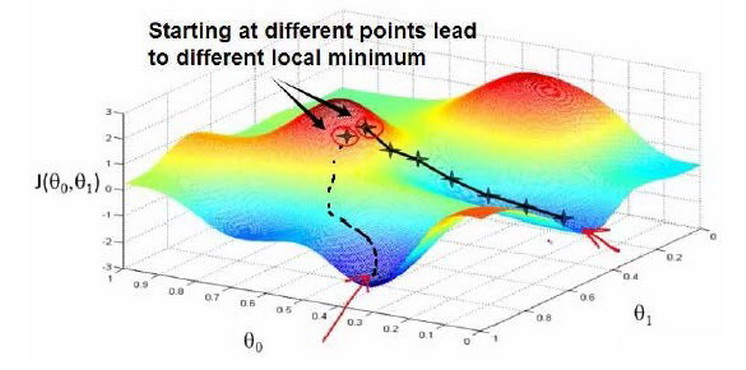
更多特征值的情况下，高维空间难以图形化，损失函数在不同区域有不同的极值，一般较难计算出最小值。

Gradient Descent

我们通常采用梯度下降算法来求的这个最小值。先随机选择一个参数组合，计算损失函数，然后找下一个能让损失函数下降最多的新参数组合并同步更新，继续这么做直到找到一个局部最小值。不同的初始参数组合可能会找到不同的局部最小值。

ai_cost_gradient_descent

梯度下降算法公式：

ai_cost_gradient_descent2

其中α是学习率(learning rate)，α决定了沿着使得损失函数下降较大的方向迈出的步子有多大，值太小则收敛太慢，值太大则可能越过最小值，导致无法收敛或者无法找到合理的待定参数组合θ。

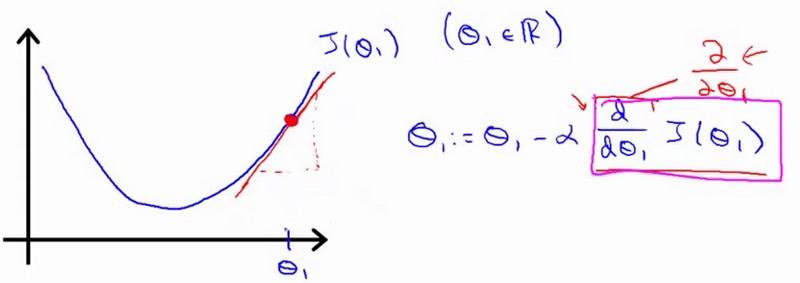
ai_cost_gradient_descent3

α右边是一个导数项，需要导数、偏导数的基础知识，简单来讲就是通过当前θ处的切线斜率来决定正确的方向，并配合学习率决定走多远。

我们现在用TensorFlow实现并体验下机器学习的思想。

准备数据

首先通过numpy生成一些模拟数据并有意随机偏移点(xi,yi)，把生成的随机点当做数据集，并把数据集按照8:2的比例分成训练集与测试集，然后通过代码去读取训练集并更新欲求参数k、b，使得k、b越来越接近真实值，使得f(xi)≈yi，从而使得方差最小。

方差对应了欧几里得距离，最小二乘法就是试图找到一条直线，使所有样本到直线上的欧氏距离之和最小。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import tensorflow as tf
import numpy as np
from tensorflow.python.framework import ops
import matplotlib.pyplot as plt

ops.reset_default_graph()

sess = tf.Session()

data_amount = 101 # 数据数量
batch_size = 25 # 批量大小

# 造数据 y=Kx+3 (K=5)
x_vals = np.linspace(20, 200, data_amount)

y_vals = np.multiply(x_vals, 5)
y_vals = np.add(y_vals, 3)

# 生成一个N(0,15)的正态分布一维数组
y_offset_vals = np.random.normal(0, 15, data_amount)
y_vals = np.add(y_vals, y_offset_vals) # 为了有意使的y值有所偏差

模型训练

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# 创建占位符
x_data = tf.placeholder(shape=[None, 1], dtype=tf.float32)
y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32)

# 构造K 就是要训练得到的值
K = tf.Variable(tf.random_normal(mean=0, shape=[1, 1]))

calcY = tf.add(tf.matmul(x_data, K), 3)

# 真实值与模型估算的差值
loss = tf.reduce_mean(tf.square(y_target - calcY))

init = tf.global_variables_initializer()
sess.run(init)

my_opt = tf.train.GradientDescentOptimizer(0.0000005)
train_step = my_opt.minimize(loss) # 目的就是使损失值最小

loss_vec = [] #保存每次迭代的损失值，为了图形化

for i in range(1000):
    rand_index = np.random.choice(data_amount, size=batch_size)
    x = np.transpose([x_vals[rand_index]])
    y = np.transpose([y_vals[rand_index]])
    sess.run(train_step, feed_dict={x_data: x, y_target: y})

    tmp_loss = sess.run(loss, feed_dict={x_data: x, y_target: y})
    loss_vec.append(tmp_loss)
# 每25的倍数输出往控制台输出当前训练数据供查看进度
    if (i + 1) % 25 == 0:
        print('Step #' + str(i + 1) + ' K = ' + str(sess.run(K)))
        print('Loss = ' + str(sess.run(loss, feed_dict={x_data: x, y_target: y})))

# 当训练完成后k的值就是当前的得到的结果，可以通过sess.run(K)取得
sess.close()

学习框架会使用梯度下降法去寻找一个最优解, 使得方差最小。

学习率是个很重要的参数，如果过小，算法收敛耗时很长，如果过大，可能结果不收敛或者直接NAN无法得到结果。

展示结果

本次试验用到了numpy及matplot，后续再练习下这两个库的使用，加强下印象。

1
2
3
4
5
6
7
8
9
10
11
best_fit = []
for i in x_vals:
    best_fit.append(KValue * i + 3)

plt.plot(x_vals, y_vals, 'o', label='Data')
plt.plot(x_vals, best_fit, 'r-', label='Base fit line')
# plt.plot(loss_vec, 'k-')
plt.title('Batch Look Loss')
plt.xlabel('Generation')
plt.ylabel('Loss')
plt.show()

图形化后有两张图，一张表示本次训练最后拟合直线，一张表示每次训练损失值的收敛情况，但结果不是唯一的。

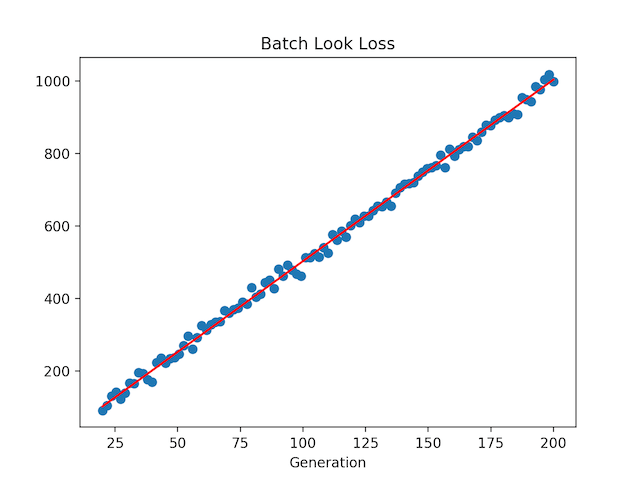
ai_kai_line_only_mul_batch_line

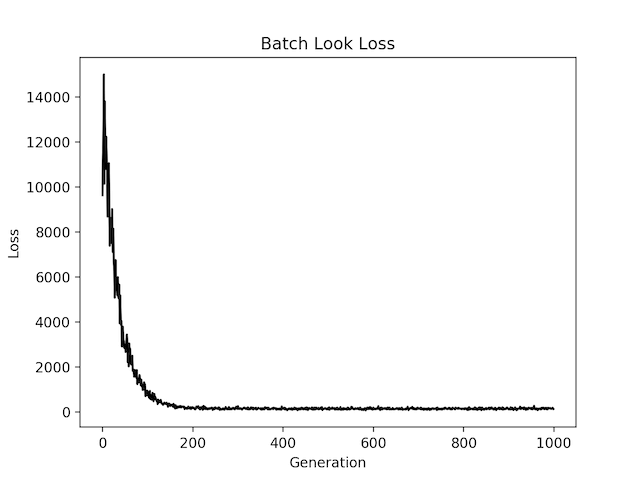
ai_kai_line_only_mul_batch_loss

可以看出，随着训练的进行，预测损失整体越来越小，改变学习率或者批量大小则会使训练损失收敛速度发生显著变化，甚至无法收敛，总体上批量数值越大效果越好。

其他回归算法

除了线性回归算法，还有其它好几种回归算法，后续陆续学习、补充。

戴明回归算法

最小二乘线性回归算法是最小化到回归直线的竖直距离，只考虑y值，而戴明回归算法是最小化到回归直线垂直距离，同时考虑x值与y值。

具体算法修改下相减的损失函数即可，两者计算结果基本一致。

lasso回归与岭回归算法

主要是在公式中增加正则项来限制斜率，lasso回归增加L1正则项，岭回归增加L2正则项。

弹性网络回归算法

综合lasso回归和岭回归的一种算法，在损失函数中同时增加L1和L2正则项。

逻辑回归算法

将线性回归转换成一个二值分类器，通过sigmoid函数将线性回归的输出缩放到0、1之间，判断目标是否属于某一类。

参考

http://studentdeng.github.io/blog/2014/07/28/machine-learning-tutorial/

　

本文首发于钱凯凯的博客 : http://qianhk.com/2018/02/客户端码农学习ML-用TensorFlow实现线性回归算法/

发布于 
tags:
  • { AI }
  • { Tensorflow }
  • { Linear Regression }